Calculate the gravity constant with Open CV

Or the standard acceleration due to gravity, or acceleration of free fall, take your pick

Summary

I was trying to find a little project to do with OpenCV that was simple enough to do in one day and didn’t require a lot of videos or calculations.
So today we are going to calculate g in a way that Newton never imagined.

All the code is in github.

Requirements:

• A known distance
  In my case it was the distance from the ceiling to the floor inside the house measured with a tape measure, 232cm

• A small red ball
  Anything will do as long as it is red-ish and made of plastic or heavier. I couldn’t find any ball so I used the Sun from an orrery my daughter painted years ago.
  My “ball” is 4cm in diameter.

• A camera with slow motion video
  I used a Google Pixel 9 Pro XL

That’s it. Let’s dig in.

Will it work over a small distance?

I am going to do my slow-motion video inside the house. Before starting, it is important to see if I will be able to get a meaningful result working “indoors”.

I am hoping to get at least 10 measurements.

The distance to my ceiling is 232cm. Since we are going to measure the center of the ball and the ball is 4cm, the real distance the center of the ball travels is 228cm.

The time the ball will travel in free fall in straight line without air resistance with d=2.28m and g=9.81m/s²

\(d = \frac{1}{2}gt^2 \implies t = \sqrt{\frac{2d}{g}} \approx 0.6818s\)

And the fps if we have 10 measurements (frames):

\(fps \geq \frac{N}{t} \implies fps \geq \frac{10}{0.6818} \approx 15\)

This is not counting for motion blur in the video or any other issues, so in practice I wouldn’t do it with less than 60fps and hoping that I can get 10 good measurements.

So yes, it will work trying this indoors, but obviously we would get better results with a bigger distance.

Taking the video

You can prepare the tripod with the camera/mobile but at the end it is just easier to ask someone to take the video. A lot of mobiles have slow motion video however not all the video is slo-mo, they tend to play at normal speed, later slo-mo and ending with normal speed (timing drift), so trying to get the right time the slow-mo starts and dropping the ball was quite difficult. Luckily the Google Pixel 9 XL Pro had the correct slo-mo settings.

The most important thing with the phone in one hand is, apart from a steady hand, not to tilt the phone (we will correct for that later).

Make sure as well to take the picture far away and that the floor and the ceiling are visible.

My dog looking at the ball falling

Hint: try to crop the video as much as possible with the mobile, it will be a lot easier than using software on the computer.

Selecting the start and end frames manually

Once we have the video it is time to check which frames are the important ones for us to start the analysis. I did the mistake at the beginning of not checking this and because the ball was bouncing after reaching the floor my g was really far from the real value.

In the github project there is a little tool I made to grab the correct frames, manual_frame_selection.py

You play frame by frame and when you see the ball about to fall down, press s (start frame) and when the ball hits the ground press e (end frame). See the video above.

For clarity, in the video I have the original recording on the left, the mask that OpenCV sees and the original recording and the mask together on the right. This way it is easy to get the best frames.

Also if the video is too big for the screen there is a scaling parameter. I needed this because my video was shot vertically and Full HD height in portrait (1920px) was more resolution than my monitor vertically (1080px).
Scaling of 0.5 worked well for me.

Converting pixels to meters

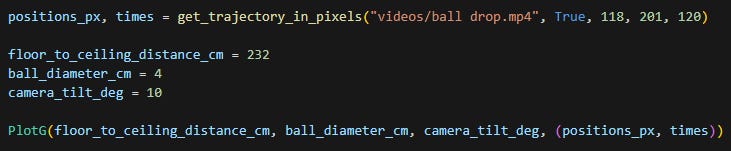
Now that we know the best starting and ending frame we need to get the trajectory in pixels. For that we have ball_drop_trajectory.py. This will give us also the times (times starting on our starting frame, not the beginning of the video).

We are almost there. In fact we can calculate the constant now but the units will be p_x/s². We assume a maximum of 10 degrees of camera tilt (I know there was some tilt but definitely no more than 10 degrees) and that’s corrected in the calculations.

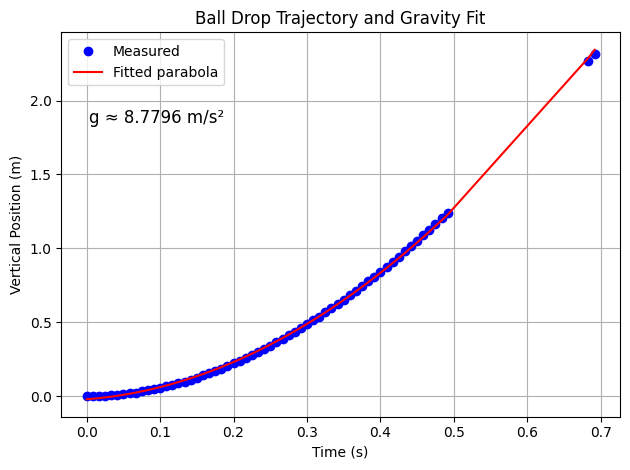
Plotting the graph and calculating g

The final step is just to plot the graph and for that we will fit to a polynomial and keep only the first coefficient since it is the one for t².

Our value for g will be:

\(\left. \begin{alignedat}{2} d &= \frac{1}{2} g t^2 \\ y(t) &= a t^2 + b t + c \end{alignedat} \quad \right\} \quad \frac{1}{2}g = a \implies g = 2a\)

With the use of numpy polyfit we estimate a value of approx. 8.78m/s².

Lies, lies and statistics

The discrepancy between our value and the real g is over 10%.

\(\text{Relative Error} = \frac{9.81 - 8.78}{9.81} \approx 10.5\%\)

Our code has been done in different classes each with one single responsibility so it is really easy, before we go any further, to play around with the values and see which one can affect g the most.

By shifting the frames one single frame to the left, from 118-201 to 117-200 we automatically get g=9.20m/s².
This is a great improvement and that tells us that having the ball drop for a very short distance introduces a really big error, specially in the starting and end points.

By changing as well the distance from floor to ceiling from 232cm to 232.5cm (which is reasonable assuming a tape measure), now g is 9.22m/s².
Again, with such a short distance any error in measurement is skewing the data greatly.

Finally what if the tilt was different than 10 degrees? 10 degrees is already a lot but if, for argument’s sake together with everything else we do a 20 degrees instead of 10 suddenly gravity is around 9.40m/s².

In short, it is really easy to tweak values slightly and have a great impact in the final result. Also we did only one try we should have done more but I couldn’t get the camera slo-mo to do the video correctly more than once, either this or the ball didn’t fall vertically.

At the end, these are the possible causes I can think of why the results are not what I expected:

• Incorrect distance measured
  Either by selecting the wrong frames, wrong measurement of the floor to ceiling distance or ball not falling in a vertical line.

• Incorrect time measured (fps)
  If the fps have a variable frame rate (timing drift) this can have a significant impact on the values for the time component.

• Camera misalignment and lens distortion
  If the camera/mobile is not on a tripod it is possible that the video is not shot fully vertically. The lens distortion by using a mobile is negligible in our case.

Conclusion and further experiments

It was a lot of fun to calculate g and disappointed with the value not being close to the real one.

For further experiments we can try with a tennis ball (or something of similar size) and throwing it from a second floor window. However for this the camera has to be a lot further and the set up can be complicated.

You can find the code in github.